Snub dodecahedron

(A possible revision to page snub dodecahedron , Section: Surface area and volume)
Snub dodecahedron

Surface area and volume

For a snub dodecahedron whose edge length is 1, the surface area is

[math]A = 20\sqrt{3} + 3\sqrt{25+10\sqrt{5}} \approx 55.286\,744\,958\,445\,15[/math].

Its volume is, putting [math]\eta=\varphi/\xi = \sqrt[3]{ \frac{\varphi}{2} + \frac{1}{2} \sqrt{\varphi-\frac{5}{27}}}\;+\; \sqrt[3]{ \frac{\varphi}{2} - \frac{1}{2} \sqrt{\varphi-\frac{5}{27}}}[/math],

[math]V= \frac{12\eta^2(3\varphi+1)-\eta(36\varphi+7)-(53\varphi+6)}{6\sqrt{3-\eta^2}^3} \approx 37.616\,649\,962\,733\,36[/math].

Or the snub dodecahedron alternate solution

[math] \text{V =}\;\frac{10\varphi}{3}\sqrt{\varphi^2+3\eta(\varphi+\eta)} \,+\,\frac{\varphi^2}{2}\sqrt{ 5 + 5\sqrt{5}\varphi\eta(\varphi +\eta)}\approx 37.616\,649\,962\,733\,36 [/math].

Its circumradius is (rest of section...)


(A version of a possible new page: snub dodecahedron alternate solution )
Snub dodecahedron alternate solution

Background

Conventional solutions to many polyhedra including the Snub Dodecahedron were made by one of the world's finest and most eloquent geometers Harold Scott MacDonald Coxeter. The golden ratio, [math]\color{Goldenrod}{\varphi}[/math], demonstrates exquisiteness in that the Snub Dodecahedron has an alternate solution method yielding a surprisingly different expression, both expressions are the same number, 37.61664996273336...

[math]\text{Conventional solution =}\; \frac{12\color{Crimson}{\eta^2}\color{Black}{(3}\color{Goldenrod}{\varphi} \color{Black}{+1)-}\color{Crimson}{\eta} \color{Black}{(36}\color{Goldenrod}{\varphi} \color{Black}{+7)-(53}\color{Goldenrod}{\varphi} \color{Black}{+6)}}{6\sqrt{(3-\color{Crimson}{\eta^2}\color{black}{)^3}}} \\ \text{Alternate solution =}\; \frac{10\color{Goldenrod}{\varphi}}{3}\sqrt{ \color{Goldenrod}{\varphi^2} \color{Black}{+3}\color{Crimson}{\eta} \color{Black}{(}\color{Goldenrod}{\varphi} \color{Black}{+}\color{Crimson}{\eta} \color{Black}{)}} \,+\,\frac{\color{Goldenrod}{\varphi^2}}{2}\sqrt{ 5 + 5\sqrt{5}\color{Goldenrod}{\varphi}\color{Crimson}{\eta} \color{Black}{(}\color{Goldenrod}{\varphi} \color{Black}{+}\color{Crimson}{\eta} \color{Black}{)}} \\ \text{where } \color{Crimson}{Eta}\text{ is defined as:} \quad \color{Crimson}{\eta\,\equiv\, \sqrt[3]{ \frac{ \color{Goldenrod}{\varphi} \color{Crimson}{}}{2} + \frac{1}{2} \sqrt{ \color{Goldenrod}{\varphi} \color{Crimson}{-}\frac{5}{27}}}\;+\;} \color{Crimson}{ \sqrt[3]{ \frac{ \color{Goldenrod}{\varphi} \color{Crimson}{}}{2} - \frac{1}{2} \sqrt{ \color{Goldenrod}{\varphi} \color{Crimson}{-}\frac{5}{27}}}} [/math]

Alternate Solution

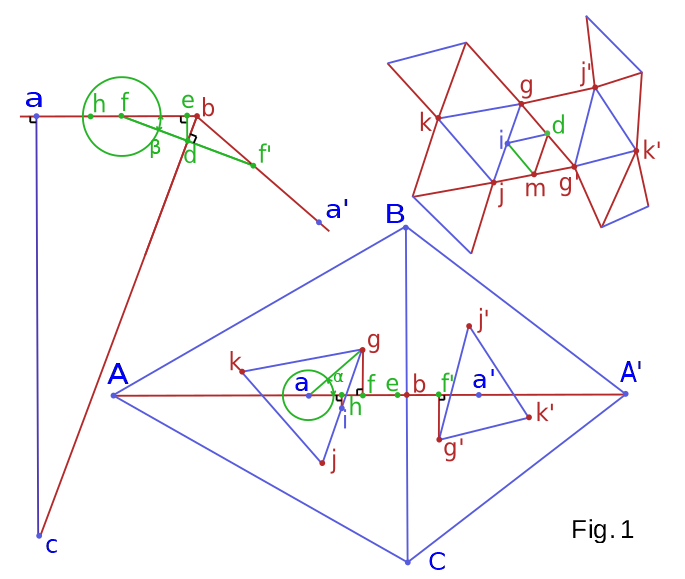
[math] \text{The Snub Dodecahedron is inscribed on to its base icosahedron of unit edge length.} \\ [/math]

[math] \begin{subarray}{ll} Base\,Icosahedron\,faces:\quad \color{blue}{\triangle A\,B\,C,\; \triangle A\prime \,B\,C} & \color {blue}{\overline{AB}} \,=\, \color {blue}{\overline{BC}} \,=\, \color {blue}{\overline{CA}} \,=\, \color {blue}{\overline{A\prime}B} \,=\, \color {blue}{\overline{CA\prime}} \,=\, 1 \\ Inscribed\,Snub\,Dodecahedron\,faces:\quad \color {blue}{\triangle g\,j\,k,\; \triangle g\prime\,j\prime\,k\prime} & \color {red}{\overline{gj}} \,=\, \color {red}{\overline{jk}} \,=\, \color {red}{\overline{kg}} \,=\, \color {red}{\overline{gg\prime}} \,=\, \color {red}{\overline{g\prime j}} \,=\, \color{green}{D\,=\, \sqrt{3}\sin\alpha-\cos\alpha} \\ Non\,Inscribed\,Snub\,Dodecahedron\,faces:\quad \color {red}{\triangle g\,g\prime\,j,\; \triangle g\prime\,g\,j\prime} & \overline{\color {red}{g}\color {blue}{i}} \,=\, \overline{\color {blue}{i}\color {red}{j}} \,=\, \overline{\color {blue}{i}\color {green}{d}} \,=\, \overline{\color {red}{g}\color {green}{d}} \,=\, \overline{\color {green}{d}\color {red}{g\prime}} \,=\, \color{green}{\frac{D}{2}} \\ Mid\,points\,on\, \color {red}{\triangle g\,g\prime\,j}:\quad\color {blue}{i} \; \color {green}{d} \; \color {red}{m} & \color{red}{ \overline{\color{blue}{a}\color{green}{f}}^2} \,+\, \color{red}{ \overline{\color{green}{f}\color{red}{g}}^2} \,=\, \color{blue}{ \overline{\color{blue}{a}\color{red}{g}}^2} \,=\, \color{green}{\frac{D^2}{3}} \\ Center\,point\,for\,both\,\color {blue}{\triangle A\,B\,C\,and\,\triangle g\,j\,k:\quad a} & \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}^2} \,+\, \color{blue}{ \overline{\color{green}{h}\color{blue}{i}}^2} \,=\, \color{blue}{ \overline{\color{blue}{a}\color{blue}{i}}^2} \,=\, \color{green}{\frac{D^2}{12}} \\ Center\,point\,for\,both\,\color {blue}{\triangle A\prime\,B\,C\,and\,\triangle g\prime\,j\prime\,k\prime:\quad a\prime} & \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}} \,=\, \color{blue}{ \overline{ai}\cos(60-\alpha)} \,=\, \color{green}{\frac{D}{4\sqrt{3}} (\cos\alpha+\sqrt{3}\sin\alpha)} \\ Center\,point\,for\,both\,Icosahedron\,and\,Snub Dodecahedron:\quad \color{blue}{c}\quad\quad & \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,=\, \color{blue}{ \overline{a\color{red}{g}}\cos\alpha} \,=\, \color{green}{ \frac{D}{ \sqrt{3}}\cos\alpha} \\ Right\,angles:\quad \color{green}{\angle} \color{green}{f}\color{green}{e}\color{green}{d}\; \color{green}{\angle} \color{green}{f}\color{green}{d}\color{red}{b}\; \color{blue}{\angle} \color{blue}{a}\color{green}{f}\color{red}{g}\; \color{green}{\angle} \color{blue}{a}\color{green}{h}\color{blue}{i}\; \color{blue}{\angle} \color{blue}{a\prime}\color{green}{f\prime}\color{red}{g\prime}\; & \color{red}{ \overline{\color{green}{f}\color{red}{b}}} \,=\, \color{red}{ \overline{\color{blue}{a}\color{red}{b}}} \,-\, \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,=\, \color{green}{\frac{1}{2\sqrt{3}} (1-2D\cos\alpha}) \\ Distance\,of\,the \,Snub\,Dodecahedron\,edge:\quad\color{green}{D} & \color{red}{ \overline{ \color{green}{e}\color{red}{b}} } \,=\, \color{red}{ \overline{ \color{green}{d}\color{red}{b}} \,sin\beta} \,=\, \color{red}{ \overline{ \color{green}{f}\color{red}{b}} \,sin^2\beta} \\ & \color{red}{ \overline{ \color{green}{e}\color{red}{b}}^2 } \,+\, \color{blue}{ \overline{ \color{green}{e}\color{green}{d}}^2} \,=\, \color{red}{ \overline{ \color{green}{e}\color {red}{b}}^2} \, (\color{red}{1+}\color{blue}{\cot^2\beta} \color{red}{)} \,=\, \color{red}{ \overline{ \color{green}{e}\color{red}{b}}}\, \color{red}{ \overline{ \color{green}{f}\color{red}{b}}} \\ \end{subarray} [/math]

[math] \text{Equations 1 and 2 are second order equations of} \;\color{green}{D}. \\ \quad \color{red}{ \overline{\color{red}{g}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\, \color{red}{ \overline{\color{red}{g}\color{green}{f}}^2} \,+\, \color{blue}{ ( \overline{\color{blue}{a}\color{red}{b}}} \,-\, \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,-\, \color{green}{ \overline{\color{green}{e}\color{red}{b}} )^2 } \,+\, \color{green}{ \overline{\color{green}{e}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{blue}{ \overline{\color{blue}{a}\color{red}{g}}^2} \,+\, \color{blue}{ \overline{\color{blue}{a}\color{red}{b}}^2} \,-\, \color{blue} {2\,\overline{\color{blue}{a}\color{red}{b}}} \, \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,+\, \color{green} { \overline{\color{green}{e}\color{red}{b}} \, \lbrack } \, \color{blue}{2\,\overline{\color{blue }{a}\color{green}{f}}} \,-\, \color{blue}{2\,\overline{\color{blue }{a}\color{red }{b}}} \,+\, \color{green}{ \overline{\color{green}{f}\color{red}{b}} \rbrack }\,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{red}{ \frac{D^2}{3} \,+\, \frac{1}{12} \,-\, \frac{D}{3} \, \cos\alpha \,+\, } \color{red}{ \sin^2\beta \, \frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}}} \color{red}{ \left[ \frac{2\,D\cos\alpha}{\sqrt{3}} \,-\, \frac{1}{\sqrt{3}} \,+\, \frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}} \right] } \,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \color{red}{ D^2 \,-\, 4D\,\cos\alpha \,+\, 1 \,-\, \sin^2\beta \,(1 \,-\, 2\,D\,\cos\alpha)^2 \,=\, 0 \quad(Eq.1)} \\ \quad \color{blue}{ \overline{\color{blue}{i}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\, \color{green}{ \overline{\color{green}{h}\color{blue}{i}}^2} \,+\, \color{blue}{ ( \overline{\color{blue}{a}\color{red}{b}}} \,-\, \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}} \,-\, \color{green}{ \overline{\color{green}{e}\color{red}{b}} } \color{blue }{)^2} \,+\, \color{green}{ \overline{\color{green}{e}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{blue}{ \overline{\color{blue}{a}\color{blue}{i}}^2} \,+\, \color{blue}{ \overline{\color{blue}{a}\color{red}{b}}^2} \,-\, \color{blue} {2\,\overline{\color{blue}{a}\color{red}{b}}} \, \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}} \,+\, \color{green} { \overline{\color{green}{e}\color{red}{b}} \, \lbrack } \, \color{blue}{2\,\overline{\color{blue }{a}\color{green}{h}}} \,-\, \color{blue}{2\,\overline{\color{blue }{a}\color{red }{b}}} \,+\, \color{green}{ \overline{\color{green}{f}\color{red}{b}} \rbrack }\,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{blue}{ \frac{D^2}{12} \,+\, \frac{1}{12} \,-\, \frac{D}{12} \, (\cos\alpha \,+\, \sqrt{3}\sin\alpha) \,+\, } \color{blue}{ \sin^2\beta \, \frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}}} \color{blue}{ \left[ \frac{D(\cos\alpha \,+\, \sqrt{3}\sin\alpha)}{2\sqrt{3}} \,-\, \frac{1}{\sqrt{3}} \,+\,\frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}}\right]}\,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \color{blue}{ -2D^2 \,-\, D\,(\cos\alpha \,+\, \sqrt{3}\sin\alpha) \,+\, 1 \,-\, \sin^2\beta \,(1 \,-\, 2\,D\,\cos\alpha) \,} \color{blue}{ \left[ 1 \,+\, D\,(\cos\alpha \,+\, \sqrt{3}\sin\alpha) \right] \,=\, 0 \quad(Eq.2)} \\ [/math]

[math] \\ \text{Equations 3 and 4 are trigonometric operators defining gamma letters:} \;\color{red}{\gamma}\;\text{and}\;\color{blue}{\Gamma}. \\ \color{red}{\gamma \,\equiv\,\sqrt{3}\,\tan\alpha} \quad \color{blue}{\Gamma \,\equiv\,3\cos\alpha-\sqrt{3}\,\sin\alpha} \\ \color{blue}{\cos^2\alpha} \,+\, \color{red}{\sin^2\alpha} \,=\, 1 \,=\, \color{blue}{\cos^2\alpha \left(1 \,+\, \color{red}{\frac{\gamma^2}{3}}\right) } \quad or \quad \color{blue}{ \cos^2\alpha\,=\,\frac{1}{ 1 \,+\, \color{red}{ \frac{\gamma^2}{3}} }} \\ \color{blue}{ \Gamma\,\cos\alpha \,=\, (\cos\alpha -\color{red}{\sqrt{3}\sin\alpha}) \cos\alpha }\,=\, \color{blue}{ (3 \,-\, \color{red}{\gamma}) \, \cos^2\alpha \,=\, \frac{3\,-\,\color{red}{\gamma}}{1 \,+\, \color{red}{ \frac{\gamma^2}{3}} }} \\ \color{red}{ 3 \left( 1 \,+\, \frac{\gamma^2}{3} \right)} \color{red}{ \left[ \color{blue}{\Gamma\,\cos\alpha\,-\,} \color{blue}{ \frac{3\,-\,\color{red}{\gamma}}{1 \,+\, \color{red}{ \frac{\gamma^2}{3}} }} \right]} \,=\, \color{red}{ \overbrace{\Gamma\,\cos\alpha}^{a}\;\gamma^2 \,+\, \overbrace{3}^{b}\;\gamma + \overbrace{3( \Gamma\,\cos\alpha\,-\,3)}^{c} }\,=\,0 \\ Positive\,Root:\;\color{red}{ \gamma \,=\, \frac{-b+\sqrt{b^2-4\,a\,c}}{2\,a} } = \color{red}{ \frac{ -3 + \sqrt{ 9-12\,\Gamma\cos\alpha(\Gamma\cos\alpha -3)}}{2\Gamma\,\cos\alpha} \quad(Eq.3) } \\ \color{blue}{ \Gamma^2 \,=\, \Gamma\,\cos\alpha \,(3 - \gamma) }\,=\, \color{blue}{ 3\Gamma\,\cos\alpha - \frac{1}{2}\left[ -3 + \sqrt{ 9-12\,\Gamma\cos\alpha(\Gamma\cos\alpha -3)} \right] \quad (Eq. 4)} \\ [/math]

[math] \text{Combine Equations 1 and 2 with variable y to solve between D and }\alpha \\ \color{Goldenrod}{ Golden\,Ratio\,phi:\;\varphi\,\equiv\, \frac{1+\sqrt{5}}{2} } \quad\quad\color{red}{ Icosa\,symmetry:\;\sin^2\beta\,=\,\frac{1}{3\varphi^2}} \\ \color{blue}{Combine:}\quad\color{blue}{ 3\varphi^2(Eq.2)} \;+\; \color{red}{3\varphi^2(Eq.1) \color{green}{y}} \,=\,0 \\ \color{green}{\overbrace{\left[3\varphi^2(y-2)+2\left((1-2y)\cos\alpha-\sqrt{3}\sin\alpha\right)\cos\alpha\right]}^{i}\,D^2 \,-\,} \color{green}{\overbrace{\left((4y+1)\cos\alpha+\sqrt{3}\sin\alpha\right)\varphi^4}^{j}\,D\;+} \color{green}{\overbrace{(y+1)\varphi^4}^{k}}\,=\,0 \\ \color{green}{Define}\,\color{red}{mu}\,and\,\color{blue}{lambda:}\; \color{green}{j^2-4ik \,\equiv\,(} \color{red}{\mu}\color{green}{\cos\alpha\,+\,} \color{blue}{\lambda}\color{green}{\sqrt{3}\sin\alpha)^2\;=\;} \color{blue}{\mu^2}\color{green}{\cos^2\alpha\,+\,} \color{red}{(\mu\lambda)} \color{green}{2\sqrt{3}\cos\alpha\sin\alpha +} \color{blue}{\lambda^2}\color{green}{3\sin^2\alpha} \\ \color{blue}{ \underbrace{ \left[ \varphi^2(4y+1)^2-4\varphi^2(y+1)\left(3\varphi^2(y-2)+2(1-2y)\right)\right]}_{\mu^2} } \color{green}{\cos^2\alpha \,+\,} \color{red}{ \underbrace{ \left[ \varphi^8(4y+1)+4\varphi^4(y+1) \right]}_{(\mu\lambda)} } \color{green}{2\sqrt{3}\cos\alpha\sin\alpha \,+\,} \color{blue}{ \underbrace{ \left[ \varphi^8-4\varphi^6(y+1)(y-2) \right]}_{\lambda^2} } \color{green}{3\sin^2\alpha} \\ Sum\,components \;\color{red}{(\mu\lambda)^2} \color{blue}{-\mu^2\lambda^2}\,=\,0 \;\color{Goldenrod}{using\;identities\quad \varphi^{n+1}-\varphi^{n-1}=\varphi^{n}\quad and \quad \varphi^{n+2}+\varphi^{n-2}=3\varphi^{n}} \\ [/math]

[math] \begin{subarray}{l} \\ \color{Goldenrod}{\varphi^{16}} &\|&&\|&&\|\; \color{red}{16}-\color{blue}{16} &&\|\; \color{red}{8}-\color{blue}{8} &&\|\; \color{red}{1}-\color{blue}{1} \\ \color{Goldenrod}{\varphi^{14}} &\|\; \color{blue}{64} &&\|\; \color{blue}{-32}\quad &&\|\; \color{blue}{-144} &&\|\; \color{blue}{-80} & \color{green}{144} &\|\; \color{blue}{-32} & \color{green}{-144} \\ \color{Goldenrod}{\varphi^{12}} &\|\; \color{blue}{-48}\quad & \color{green}{144}\; &\|\; \color{blue}{96} & \color{green}{0}\; &\|\; \color{red}{32} \color{blue}{+128}\quad & \color{green}{-288} &\|\; \color{red}{40} \color{blue}{-200} &&\|\; \color{red}{8} \color{blue}{-184}\quad & \color{green}{\;144} \\ \color{Goldenrod}{\varphi^{10}} &\|\; \color{blue}{64} &&\|\; \color{blue}{-32} &&\|\; \color{blue}{-192} &&\|\; \color{blue}{-32} &&\|\; \color{blue}{64} \\ \color{Goldenrod}{\varphi^{8}} &\|&&\|&&\|\; \color{red}{16} &&\|\; \color{red}{32} &&\|\; \color{red}{16} \\ \color{Goldenrod}{\div144\varphi^{12}} &\|& \color{green}{y^4} &\|& &\|& \color{green}{-2y^2\;} &\|& \color{green}{-\varphi^2 y\;} &\|& \color{green}{\;-\varphi} \end{subarray} \\ [/math]

[math] \begin{subarray}{lc} \color{red}{First\,root\,of\,y:\;-1} &&&\color{blue}{y^3} &\color{blue}{\overbrace{-y^2}^{p=-1}} &\color{blue}{\overbrace{-y}^{q=-1}} &\color{blue}{\overbrace{-\varphi}^{r=-\varphi}} \\ \color{blue}{a=\frac{-p^2}{3}+q\;=\; \frac{-1}{3}-1\;=\;\frac{-4}{3} }\; \color{Goldenrod}{(if\,a=\frac{2}{3},\,y\,is\,origin\,to\,\varphi^\frac{n}{3})} & \color{red}{(y+1)} &\quad \color{green}{\overline{|\;y^4}} \quad&&\quad\color{green}{-2y^2} \quad&\quad\color{green}{-\varphi^2y} \quad&\color{green}{-\varphi} \\ \color{blue}{b=\frac{2p^2}{27}-\frac{pq}{3}+r} \quad&& \color{green}{y^4} & \color{green}{+y^3} \\ \color{blue}{b=-\frac{2}{27}-\frac{1}{3}-\varphi \;=\; \frac{-49-27\sqrt{5}}{54}} \quad&& \color{green}{0} & \color{green}{-y^3} & \color{green}{-y^2} \\ \color{blue}{Second\,root\,of\,y:} \quad&&& \color{green}{0} & \color{green}{-y^2} & \color{green}{-y} \\ \color{blue}{\frac{-p}{3} -\sqrt[3]{ \frac{b}{2}+\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} -\sqrt[3]{ \frac{b}{2}-\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} \;=\; \eta^2-\frac{1}{3}} \quad&&&& \color{green}{0} & \color{green}{-\varphi y} & \color{green}{-\varphi} \\ \color{blue}{ Where\,eta\;is\,defined:\,\eta\,\equiv\,} \color{blue}{ \sqrt[3]{ \frac{\varphi}{2} + \frac{1}{2} \sqrt{ \varphi-\frac{5}{27}}}\;+\;} \color{blue}{ \sqrt[3]{ \frac{\varphi}{2} - \frac{1}{2} \sqrt{ \varphi-\frac{5}{27}}}} \quad&&&&& \color{green}{0} & \color{green}{0} \end{subarray} \\ [/math]

[math] \color{red}{From\,the\,first\,root\,of\,y:} \frac{ \color{blue}{(Eq.2)} -\color{red}{(Eq.1)}}{\color{green}{D}}\;=\;0 \\ \color{green}{ \left[ 2(3\cos\alpha-\sqrt{3}\sin\alpha)\cos\alpha-9\varphi^2\right] D \;+\; \varphi^4(3\cos\alpha-\sqrt{3}\sin\alpha)}\;=\; \color{green}{\left[ 2\Gamma\cos\alpha-9\varphi^2\right] D \;+\; \varphi^4\Gamma}\;=\;0 \\ \color{green}{D\;=\;\frac{ \varphi^4\Gamma}{9\varphi^2 - 2\Gamma\cos\alpha} \quad(Eq.5)} [/math]

[math] \color{red}{\frac{ \Gamma(9\varphi^2 - 2\Gamma\cos\alpha)}{ 3\varphi^2D} (Eq.1)} \;=\;0 \quad\color{green}{(substitute\,D\,with\,Eq.5)} \\ \color{red}{ \frac{ \Gamma(9\varphi^2 - 2\Gamma\cos\alpha)}{ 3\varphi^2}} \color{red}{\left[ (3\varphi^2-4\cos^2\alpha) \color{green}{ \left( \frac{ \varphi^4\Gamma}{9\varphi^2-2\Gamma\cos\alpha} \right)} -4\varphi^4\cos\alpha+\varphi^4 \color{green}{ \left( \frac{9\varphi^2-2\Gamma\cos\alpha}{ \varphi^4\Gamma} \right)} \right]} \;=\;0 \\ \color{red}{4(\Gamma\cos\alpha)^2 - 36\varphi^2\Gamma\cos\alpha + 27\varphi^2 + \varphi^4\Gamma^2} \;=\;0 \quad\color{blue}{(substitute\,\Gamma^2\,with\,Eq.4)} \\ \color{red}{4(\Gamma\cos\alpha)^2 + 3\varphi^2(\color{blue}{\varphi^4}-12)\Gamma\cos\alpha + \frac{3}{2}\varphi^2(\color{blue}{\varphi^2}+18)}\;=\; \color{blue}{ \frac{\varphi^4}{2}\sqrt{9-12\Gamma\cos\alpha(\Gamma\cos\alpha - 3)}} \\ \color{green}{\text{Square both sides and subtract}} \\ \color{green}{16(\Gamma\cos\alpha)^4 + 24\varphi^2(\varphi^2-12)(\Gamma\cos\alpha)^3 + 36\varphi^2(21\varphi^2 + 11)(\Gamma\cos\alpha)^2 + 54\varphi^4(\varphi^2-36)\Gamma\cos\alpha + 81\varphi^4(\varphi^2+9)}\;=\;0 \\ \color{green}{ Define\;x:\quad x\equiv\frac{2}{3}\Gamma\cos\alpha \quad \text{ and divide by 81:}} \\ \color{green}{x^4 + \varphi^2(\varphi^2-12)x^3 + \varphi^2(21\varphi^2+11)x^2 + \varphi^4(\varphi^2-36)x + \varphi^4(\varphi^2+9)}\;=\;0 \\ [/math]

[math] \begin{subarray}{lc} \color{red}{First\,root\,of\,x:\;1} &&&\color{blue}{x^3} &\color{blue}{\overbrace{-9\varphi^2}^{p=-9\varphi^2}x^2} &\color{blue}{\overbrace{+\varphi^2(21\varphi^2+2)}^{q=\varphi^2(21\varphi^2+2)}x} &\color{blue}{\overbrace{-\varphi^4(\varphi^2+9)}^{r=-\varphi^4(\varphi^2+9)}} \\ \color{blue}{a=\frac{-p^2}{3}+q\;=\; -27\varphi^4+\varphi^2(21\varphi^2+2) \;=\; -2\varphi^6 } & \color{red}{(x-1)} &\quad \color{green}{\overline{|\;x^4}} \quad&\quad\color{green}{+\varphi^2(\varphi^2-12)x^3} \quad&\quad\color{green}{+\varphi^2(21\varphi^2+11)x^2} \quad&\color{green}{+\varphi^4(\varphi^2-36)x} \quad&\color{green}{+\varphi^4(\varphi^2+9)} \\ \color{blue}{b=\frac{2p^2}{27}-\frac{pq}{3}+r} \quad&& \color{green}{x^4} & \color{green}{-x^3} \\ \color{blue}{b=-54\varphi^6 + 3\varphi^4(21\varphi^2+2) - \varphi^4(\varphi^2+9)\;=\;{\huge \color{Goldenrod}{\varphi^{10}}}} \quad&& \color{green}{0} & \color{green}{-9\varphi^2x^3} & \color{green}{+9\varphi^2x^2} \\ \quad&&& \color{green}{0} & \color{green}{\varphi^2(21\varphi^2+2)x^2} & \color{green}{-\varphi^2(21\varphi^2+2)x} \\ \color{blue}{Second\,root\,of\,x:} \quad&&&& \color{green}{0} & \color{green}{-\varphi^4(\varphi^2+9)x} & \color{green}{\varphi^4(\varphi^2+9)} \\ \color{blue}{\frac{-p}{3} -\sqrt[3]{ \frac{b}{2}+\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} -\sqrt[3]{ \frac{b}{2}-\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} \;=\; 3\varphi^2-\varphi^3\eta} &&&&& \color{green}{0} & \color{green}{0} \\ \end{subarray} \\ \color{blue}{\text{From the second root of x:} \quad \Gamma\cos\alpha \;=\; \frac{3}{2}(3\varphi^2-\varphi^3\eta)\quad(Eq.6) } \\ [/math]

[math] \color{green}{ \left( \sqrt[3]{ \frac{\varphi}{2} + \sqrt{ \frac{\varphi^2}{4}-\frac{8}{27}}}\right)} \color{green}{ \left( \sqrt[3]{ \frac{\varphi}{2} - \sqrt{ \frac{\varphi^2}{4}-\frac{8}{27}}}\right)} \color{green}{\;=\; \sqrt[3]{\frac{8}{27}} \;=\; \frac{2}{3} \quad so, \quad \eta^3 = 2\eta + \varphi\quad(Eq.7)} \\ [/math]

[math] \color{green}{Noting\;D\,=\, \sqrt{3}\sin\alpha-\cos\alpha, \;we\,find:} \\ \quad\color{red}{ (9\varphi^3+\varphi+6\eta-3\varphi^3\eta^2)^2} \color{blue}{ -(\varphi+3\eta)^2 \left(1-3\varphi^4(3\sqrt{5}-2\varphi^3\eta + \varphi^2\eta^2)\right)} \;=\;0 \quad\color{green}{(expand\,and\,substitute\,\eta^3\,with\,Eq.7)} \\ \color{green}{=\;} \color{red}{(9\varphi^3+\varphi)^2 + 36\eta^2 +9\varphi^6\eta\color{green}{(2\eta+\varphi)}+2(9\varphi^3+\varphi)(6\eta-3\varphi^3\eta^2)} \color{red}{-36\varphi^3} \color{green}{(2\eta+\varphi)} \color{blue}{ -\varphi^2 \left(1-3\varphi^4(3\sqrt{5} - 2\varphi^3\eta + \varphi^2\eta^2) \right)} \\ \quad\color{blue}{-6\varphi \left( \eta-3\varphi^4 \left( 3\sqrt{5}\eta - 2\varphi^3\eta^2 + \varphi^2\color{green}{(2\eta+\varphi)} \right)\right)} \color{blue}{-9 \left( \eta^2-3\varphi^4 \left( 3\sqrt{5}\eta^2 - 2\varphi^3\color{green}{(2\eta+\varphi)} + \varphi^2\eta\color{green}{(2\eta+\varphi)} \right)\right)}\;=\;0 \\ \color{green}{=\;(} \color{red}{81\varphi^6+18\varphi^4+\varphi^2-36\varphi^4} \color{blue}{-\varphi^2+9\varphi^6\sqrt{5}+18\varphi^8-54\varphi^8} \color{green}{)\quad\quad\text{(all 3 orders of}\;\eta\;\text{sum to zero)}} \\ \quad\color{green}{+\;(} \color{red}{9\varphi^7+12(9\varphi^3+\varphi)-72\varphi^3} \color{blue}{+6\varphi^9-6\varphi +54\varphi^5\sqrt{5}+36\varphi^7-108\varphi^8+27\varphi^7} \color{green}{)\eta} \\ \quad\quad\color{green}{+\;(} \color{red}{36+ 18\varphi^6-6\varphi^3(9\varphi^3+\varphi)} \color{blue}{+3\varphi^8-36\varphi^8-9 + 81\varphi^4 \sqrt{5}+54\varphi^6} \color{green}{)\eta^2}\;=\;0 \\ [/math]

[math] \color{blue}{\sqrt{1-3\varphi^4(3\sqrt{5}-2\varphi^3\eta+ \varphi^2\eta^2)}} \color{red}{\;=\;\frac{9\varphi^3+\varphi+6\eta-3\varphi^3\eta^2}{\color{blue}{\varphi +3\eta}}} \quad\color{blue}{(Eq.8)} \\ [/math]

[math] \color{green}{Substitute\color{blue}{Eq.6}\,and\,\color{blue}{Eq.8}\,into\,\color{red}{Eq.3}} \\ \color{red}{\gamma\;=\; \frac{ -3 + \sqrt{ 9-12\,\Gamma\cos\alpha(\Gamma\cos\alpha -3)}}{2\Gamma\,\cos\alpha}} \color{blue}{ \;=\;\frac{ -1+\sqrt{ 1-3\varphi^4(3\sqrt{5}-2\varphi^3\eta+\varphi^2\eta^2)}}{3\varphi^2-\varphi^3\eta} } \color{blue}{ \;=\;\frac{ -1+ \color{red}{\frac{9\varphi^3+\varphi+6\eta-3\varphi^3\eta^2}{\color{blue}{\varphi +3\eta}}}}{ 3\varphi^2-\varphi^3\eta}} \\ \color{red}{\gamma\;=\; \frac{ \color{blue}{-\varphi -3\eta} +9\varphi^3 +\varphi +3\eta +3(3\varphi^2 - \varphi^4)\eta -3\varphi^3\eta^2} {\color{blue}{(\varphi +3\eta)(3\varphi^2 -\varphi^3\eta) }}} \color{red}{\;=\;\frac{3\varphi+3\eta}{\varphi+3\eta}} \\ \color{blue}{ \cos\alpha \;=\; \frac{1}{ \sqrt{ 1\color{red}{+\tan^2\alpha}}}} \;=\; \color{blue}{ \frac{1}{ \sqrt{ 1\color{red}{ +\frac{\gamma^2}{3} }}}} \;=\; \color{blue}{ \frac{1}{ \sqrt{ 1\color{red}{ +\frac{1}{3}\left( \frac{3\varphi+3\eta}{\varphi+3\eta} \right)^2}}}} \;=\; \color{blue}{ \frac{\varphi+3\eta}{2\sqrt{ \varphi^2+3\eta(\varphi+\eta)}}} \\ [/math]

[math] \color{blue}{ \Gamma\;=\;\cos\alpha[3\color{red}{-\gamma}]} \color{blue}{ \;=\; \left( \frac{\varphi+3\eta}{2\sqrt{ \varphi^2+3\eta(\varphi+\eta)}} \right) } \color{blue}{ \left[ 3\color{red}{-\frac{3\varphi+3\eta}{\varphi+3\eta}} \right] } \color{blue}{ \;=\; \frac{3\eta}{\sqrt{ \varphi^2+3\eta(\varphi+\eta)}} \quad(Eq.9)} \\ [/math]

[math] \color{green}{Substitute\;\color{blue}{Eq.6}\;and\;\color{blue}{Eq.9}\;into\,Eq.5} \\ \color{green}{D\;=\;\frac{ \varphi^4\Gamma}{9\varphi^2 - 2\Gamma\cos\alpha}} \color{green}{\;=\;\frac{\varphi\Gamma}{3\eta}} \color{green}{ \;=\; \frac{\varphi}{\sqrt{ \varphi^2+3\eta(\varphi+\eta)}}} \\ [/math]

[math] \color{red}{Icosa\,symmetry:}\; \color{blue}{\cos\beta=\frac{\varphi}{\sqrt{3}}} \quad \color{red}{ \sin\beta=\frac{1}{\varphi\sqrt{3}}} \quad \color{blue}{\overline{a\color{green}{b}}=\frac{1}{2\sqrt{3}}} \quad \color{blue}{\overline{ac}=\frac{\overline{a\color{green}{b}}}{\tan\beta}= \frac{\varphi^2}{2\sqrt{3}}} \\ \color{green}{ \text{Radius to triangle face:}\;r_{triangle}\;=\; \frac{\color{blue}{\overline{ac}}}{\color{green}{D}}} \color{green}{ \;=\; \frac{\varphi}{2\sqrt{3}}\sqrt{ \varphi^2+3\eta(\varphi+\eta)}} \\ \color{green}{ \text{Circumradius (radius to vertex):}} \\ \color{green}{r_{circumradius}\;=\; \sqrt{ \color{blue}{r^2_{triangle}} \color{red}{+(2\sin\frac{\pi}{3})^{-2}} }} \color{green}{ \;=\; \sqrt{ \frac{ \color{blue}{\varphi^2\left(\varphi^2 + 3\eta(\varphi+\eta)\right)} \color{red}{+ 4}}{12} }} \color{green}{ \;=\; \frac{1}{2}\sqrt{ \frac{ \varphi^4 + 4 +3\varphi^2\eta(\varphi+\eta) }{3}}} \\ \color{green}{ \text{Inradius (radius to pentagon face):}} \\ \color{green}{r_{pentagon}\;=\; \sqrt{ \color{blue}{r^2_{circumradius}} \color{red}{-(2\sin\frac{\pi}{5})^{-2}} }} \color{green}{ \;=\; \sqrt{ \frac{ \color{blue}{ \varphi^4 + 4 +3\varphi^2\eta(\varphi+\eta) } }{12} \color{red}{-\frac{\varphi}{\sqrt{5}}} }} \color{green}{ \;=\; \frac{\varphi}{2}\sqrt{ \frac{1}{\varphi\sqrt{5}}+\eta(\varphi+\eta)}} \\ \color{green}{ \text{Midradius (radius to edge bisector):}} \\ \color{green}{r_{midradius}\;=\; \sqrt{ \color{blue}{r^2_{triangle}} \color{red}{+ (2\tan\frac{\pi}{3})^{-2}} }} \color{green}{ \;=\; \sqrt{ \frac{ \color{blue}{\varphi^2\left(\varphi^2 + 3\eta(\varphi+\eta)\right)} \color{red}{+1} }{12} }} \color{green}{ \;=\; \frac{1}{2}\sqrt{ \frac{ \varphi^4 + 1 +3\varphi^2\eta(\varphi+\eta) }{3}}} \\ \color{red}{Volume_{Snub Dodecahedron}\;=\;} \color{blue}{N_{triangle}\times Area_{triangle}\times\frac{1}{3} \times r_{triangle} } \color{green}{+N_{pentagon}\times Area_{pentagon}\times\frac{1}{3} \times r_{pentagon} } \\ \quad\color{red}{=\;} \color{blue}{ 80\frac{\sqrt{3}}{4}\frac{1}{3}\frac{\varphi}{2\sqrt{3}}\sqrt{ \varphi^2+3\eta(\varphi+\eta)}} \color{green}{\,+\,12\frac{5}{4}\sqrt{\frac{\varphi^3}{\sqrt{5}}}\frac{1}{3} \frac{\varphi}{2}\sqrt{ \frac{1}{\varphi\sqrt{5}}+\eta(\varphi+\eta)} } \\ \color{red}{Volume_{Snub Dodecahedron}\;=\;} \color{red}{\frac{10\varphi}{3}\sqrt{ \varphi^2+3\eta(\varphi+\eta)}} \color{red}{\,+\,\frac{\varphi^2}{2}\sqrt{ 5 + 5\sqrt{5}\varphi\eta(\varphi+\eta)} } \\ [/math]