Snub-dodecahedron-2
Brief history of the Snub Dodecahedron
Early History
The first known record of the Snub Dodecahedron[1] is from Pappus of Alexandria[2] around 340 AD. In Book V of the Collection, he attributes Archimedes of Syracuse[3] (287-212 BC) as the discoverer of thirteenth semiregular polyhedra, the Archimedean Solids[4]. The Snub Dodecahedron is generally referred to as the thirteenth Archimedean solid, however MathWorld list the Snub Dodecahedron in order of Schläfli Symbol[5] progression as the eighth solid. Their beauty sparked rediscovery of the Archimedean solids during the Renaissance.[6]. and continues today. These solids are found in early works such as Luca Pacioli's[7] "De divina proportione"[8] (Venice 1509) and Johannes Kepler's[9] Harmonices Mundi [10](Linz 1619). As one of the two chiral snub solids, the Snub Dodecahedron exists in two enantiomorphous forms, commonly called laevo (left-handed) and dextro (right-handed).
Modern History
In 1954, H. S. M. Coxeter, M. S. Longuet-Higgins, and J. C. P. Miller published "Uniform Polyhedra" in the Philosophical Transactions of the Royal Society of London.[11] The Snub Dodecahedron is solved in a single line equation:
\begin{align*} X^3 + 2X^2 - \color{Goldenrod}{\varphi^2} = 0,\quad \text{where the }\color{Goldenrod}{Golden\,Ratio}\text{ is defined as:}\quad\color{Goldenrod}{\varphi\,\equiv\, \frac{1+\sqrt{5}}{2}} \quad \end{align*}
The Golden Ratio demonstrates beauty of a fantastic nature. Equally fantastic is that the Snub Dodecahedron has been solved in two completely different manners yielding two wildly different closed-form expressions:
\begin{align*} \text{Coxeter's solution =}\; \frac{12\color{Crimson}{\xi^2}\color{Black}{(3}\color{Goldenrod}{\varphi} \color{Black}{+1)-}\color{Crimson}{\xi} \color{Black}{(36}\color{Goldenrod}{\varphi} \color{Black}{+7)-(53}\color{Goldenrod}{\varphi} \color{Black}{+6)}}{6\sqrt{(3-\color{Crimson}{\xi^2}\color{black}{)^3}}} \end{align*}
\begin{align*}
\text{Adams' solution =}\;
\frac{10\color{Goldenrod}{\varphi}}{3}\sqrt{ \color{Goldenrod}{\varphi^2}
\color{Black}{+3}\color{Crimson}{\xi}
\color{Black}{(}\color{Goldenrod}{\varphi}
\color{Black}{+}\color{Crimson}{\xi}
\color{Black}{)}}
\,+\,\frac{\color{Goldenrod}{\varphi^2}}{2}\sqrt{ 5 + 5\sqrt{5}\color{Goldenrod}{\varphi}\color{Crimson}{\xi}
\color{Black}{(}\color{Goldenrod}{\varphi}
\color{Black}{+}\color{Crimson}{\xi}
\color{Black}{)}}
\\
\end{align*}
\begin{align*}
\text{where } \color{Crimson}{Xi}\text{ is defined as:} \quad
\color{Crimson}{\xi\,\equiv\,
\sqrt[3]{ \frac{
\color{Goldenrod}{\varphi}
\color{Crimson}{}}{2} + \frac{1}{2} \sqrt{
\color{Goldenrod}{\varphi}
\color{Crimson}{-}\frac{5}{27}}}\;+\;}
\color{Crimson}{
\sqrt[3]{ \frac{
\color{Goldenrod}{\varphi}
\color{Crimson}{}}{2} - \frac{1}{2} \sqrt{
\color{Goldenrod}{\varphi}
\color{Crimson}{-}\frac{5}{27}}}}
\end{align*}
These two solutions are in fact the same number, as shown in this Wolfram Cloud Notebook[12]. Both equal 37.616649962733362975777673671302714340355289873488...
As one of the world's finest and most eloquent geometers, Donald Coxeter's[13] many discoveries were embraced by Eric Wolfgang Weisstein[14]. Eric derived the above closed-form expression of Coxeter's solution to include in his publications. In 2010, an unknown party copied his expression to Wikipedia where it has propagated elsewhere. In MathWorld, Eric presents the Snub Dodecahedron volume in the more principle open-form expression that may be used to derive the closed-form:
\begin{align*}
&\small{187445810737515625 -
182124351550575000\,x^2 +
6152923794150000\,x^4 +}
\\&
\small{1030526618040000\,x^6 +
162223191936000\,x^8 -
3195335070720\,x^{10} +
2176782336\,x^{12} = 0}
\\
\end{align*}
Harish Chandra Rajpoot published his 2015 paper, Optimum Solution of Snub Dodecahedron[15]. HCR's Theory of Polygon & Newton-Raphson Method is used to calculate the volume of the Snub Dodecahedron. After only 7 iterations, the calculated volume matches the closed-form solutions to 50 digits of accuracy:
\begin{align*} \\& Iterate\,to\,find\,Circumradius\quad C_{0} = 2.3\quad C_{n+1}=\frac{f(C_{n})}{f\prime (C_{n})} \\& f(x)= 256(3-\sqrt{5})x^8 - 128(13-2\sqrt{5})x^6 + 32(35-3\sqrt{5})x^4 - 16(19-\sqrt{5})x^2 +(29-\sqrt{5}) \\& f\prime(x)= 2048(3-\sqrt{5})x^7 - 768(13-2\sqrt{5})x^5 + 128(35-3\sqrt{5})x^3 - 32(19-\sqrt{5})x \\& Volume = \left( \frac{20\sqrt{3C^2-1}}{3} + \sqrt{ \frac{10(5+2\sqrt{5})C^2 - 5((7+3\sqrt{5})}{2}} \right) \end{align*}
In 1985, Mark Shelby Adams published Archimedean & Platonic Solids[16]. Equation 8 was discovered by a lucky guess on a calculator showing that √3 sin α - cos α = D. Here is his solution:
Solution of the Snub Dodecahedron
Figure 1
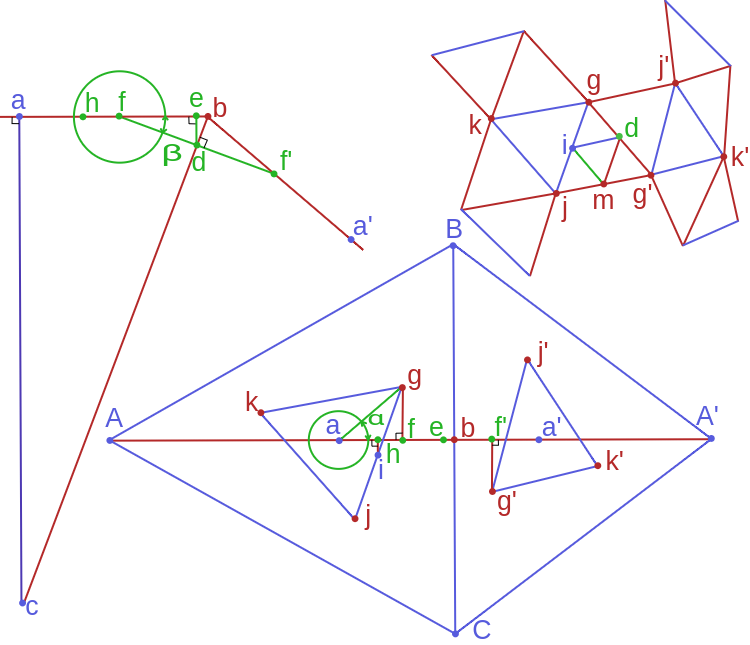
The Snub Dodecahedron is inscribed on to its base icosahedron.
Triangular faces of icosahedron and snub dodecahedron are all equilateral.
Base icosahedron is of unit edge length.
[math] \begin{subarray}{ll} Base\,Icosahedron\,faces:\quad \color{blue}{\triangle A\,B\,C,\; \triangle A\prime \,B\,C} & \color {blue}{\overline{AB}} \,=\, \color {blue}{\overline{BC}} \,=\, \color {blue}{\overline{CA}} \,=\, \color {blue}{\overline{A\prime}B} \,=\, \color {blue}{\overline{CA\prime}} \,=\, 1 \\ Inscribed\,Snub\,Dodecahedron\,faces:\quad \color {blue}{\triangle g\,j\,k,\; \triangle g\prime\,j\prime\,k\prime} & \color {red}{\overline{gj}} \,=\, \color {red}{\overline{jk}} \,=\, \color {red}{\overline{kg}} \,=\, \color {red}{\overline{gg\prime}} \,=\, \color {red}{\overline{g\prime j}} \,=\, \color{green}{D\,=\, \sqrt{3}\sin\alpha-\cos\alpha} \\ Non\,Inscribed\,Snub\,Dodecahedron\,faces:\quad \color {red}{\triangle g\,g\prime\,j,\; \triangle g\prime\,g\,j\prime} & \overline{\color {red}{g}\color {blue}{i}} \,=\, \overline{\color {blue}{i}\color {red}{j}} \,=\, \overline{\color {blue}{i}\color {green}{d}} \,=\, \overline{\color {red}{g}\color {green}{d}} \,=\, \overline{\color {green}{d}\color {red}{g\prime}} \,=\, \color{green}{\frac{D}{2}} \\ Mid\,points\,on\, \color {red}{\triangle g\,g\prime\,j}:\quad\color {blue}{i} \; \color {green}{d} \; \color {red}{m} & \color{red}{ \overline{\color{blue}{a}\color{green}{f}}^2} \,+\, \color{red}{ \overline{\color{green}{f}\color{red}{g}}^2} \,=\, \color{blue}{ \overline{\color{blue}{a}\color{red}{g}}^2} \,=\, \color{green}{\frac{D^2}{3}} \\ Center\,point\,for\,both\,\color {blue}{\triangle A\,B\,C\,and\,\triangle g\,j\,k:\quad a} & \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}^2} \,+\, \color{blue}{ \overline{\color{green}{h}\color{blue}{i}}^2} \,=\, \color{blue}{ \overline{\color{blue}{a}\color{blue}{i}}^2} \,=\, \color{green}{\frac{D^2}{12}} \\ Center\,point\,for\,both\,\color {blue}{\triangle A\prime\,B\,C\,and\,\triangle g\prime\,j\prime\,k\prime:\quad a\prime} & \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}} \,=\, \color{blue}{ \overline{ai}\cos(60-\alpha)} \,=\, \color{green}{\frac{D}{4\sqrt{3}} (\cos\alpha+\sqrt{3}\sin\alpha)} \\ Center\,point\,for\,both\,Icosahedron\,and\,Snub Dodecahedron:\quad \color{blue}{c}\quad\quad & \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,=\, \color{blue}{ \overline{a\color{red}{g}}\cos\alpha} \,=\, \color{green}{ \frac{D}{ \sqrt{3}}\cos\alpha} \\ Right\,angles:\quad \color{green}{\angle} \color{green}{f}\color{green}{e}\color{green}{d}\; \color{green}{\angle} \color{green}{f}\color{green}{d}\color{red}{b}\; \color{blue}{\angle} \color{blue}{a}\color{green}{f}\color{red}{g}\; \color{green}{\angle} \color{blue}{a}\color{green}{h}\color{blue}{i}\; \color{blue}{\angle} \color{blue}{a\prime}\color{green}{f\prime}\color{red}{g\prime}\; & \color{red}{ \overline{\color{green}{f}\color{red}{b}}} \,=\, \color{red}{ \overline{\color{blue}{a}\color{red}{b}}} \,-\, \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,=\, \color{green}{\frac{1}{2\sqrt{3}} (1-2D\cos\alpha}) \\ Distance\,of\,the \,Snub\,Dodecahedron\,edge:\quad\color{green}{D} & \color{red}{ \overline{ \color{green}{e}\color{red}{b}} } \,=\, \color{red}{ \overline{ \color{green}{d}\color{red}{b}} \,sin\beta} \,=\, \color{red}{ \overline{ \color{green}{f}\color{red}{b}} \,sin^2\beta} \\ & \color{red}{ \overline{ \color{green}{e}\color{red}{b}}^2 } \,+\, \color{blue}{ \overline{ \color{green}{e}\color{green}{d}}^2} \,=\, \color{red}{ \overline{ \color{green}{e}\color {red}{b}}^2} \, (\color{red}{1+}\color{blue}{\cot^2\beta} \color{red}{)} \,=\, \color{red}{ \overline{ \color{green}{e}\color{red}{b}}}\, \color{red}{ \overline{ \color{green}{f}\color{red}{b}}} \\ \end{subarray} [/math]
Equations 1 and 2
Equations 1 and 2 are second order equations of D [math] \quad \color{red}{ \overline{\color{red}{g}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\, \color{red}{ \overline{\color{red}{g}\color{green}{f}}^2} \,+\, \color{blue}{ ( \overline{\color{blue}{a}\color{red}{b}}} \,-\, \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,-\, \color{green}{ \overline{\color{green}{e}\color{red}{b}} )^2 } \,+\, \color{green}{ \overline{\color{green}{e}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{blue}{ \overline{\color{blue}{a}\color{red}{g}}^2} \,+\, \color{blue}{ \overline{\color{blue}{a}\color{red}{b}}^2} \,-\, \color{blue} {2\,\overline{\color{blue}{a}\color{red}{b}}} \, \color{blue}{ \overline{\color{blue}{a}\color{green}{f}}} \,+\, \color{green} { \overline{\color{green}{e}\color{red}{b}} \, \lbrack } \, \color{blue}{2\,\overline{\color{blue }{a}\color{green}{f}}} \,-\, \color{blue}{2\,\overline{\color{blue }{a}\color{red }{b}}} \,+\, \color{green}{ \overline{\color{green}{f}\color{red}{b}} \rbrack }\,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{red}{ \frac{D^2}{3} \,+\, \frac{1}{12} \,-\, \frac{D}{3} \, \cos\alpha \,+\, } \color{red}{ \sin^2\beta \, \frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}}} \color{red}{ \left[ \frac{2\,D\cos\alpha}{\sqrt{3}} \,-\, \frac{1}{\sqrt{3}} \,+\, \frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}} \right] } \,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \color{red}{ D^2 \,-\, 4D\,\cos\alpha \,+\, 1 \,-\, \sin^2\beta \,(1 \,-\, 2\,D\,\cos\alpha)^2 \,=\, 0 \quad(Eq.1)} \\ \quad \color{blue}{ \overline{\color{blue}{i}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\, \color{green}{ \overline{\color{green}{h}\color{blue}{i}}^2} \,+\, \color{blue}{ ( \overline{\color{blue}{a}\color{red}{b}}} \,-\, \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}} \,-\, \color{green}{ \overline{\color{green}{e}\color{red}{b}} } \color{blue }{)^2} \,+\, \color{green}{ \overline{\color{green}{e}\color{green}{d}}^2} \,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{blue}{ \overline{\color{blue}{a}\color{blue}{i}}^2} \,+\, \color{blue}{ \overline{\color{blue}{a}\color{red}{b}}^2} \,-\, \color{blue} {2\,\overline{\color{blue}{a}\color{red}{b}}} \, \color{blue}{ \overline{\color{blue}{a}\color{green}{h}}} \,+\, \color{green} { \overline{\color{green}{e}\color{red}{b}} \, \lbrack } \, \color{blue}{2\,\overline{\color{blue }{a}\color{green}{h}}} \,-\, \color{blue}{2\,\overline{\color{blue }{a}\color{red }{b}}} \,+\, \color{green}{ \overline{\color{green}{f}\color{red}{b}} \rbrack }\,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \quad \color{blue}{ \frac{D^2}{12} \,+\, \frac{1}{12} \,-\, \frac{D}{12} \, (\cos\alpha \,+\, \sqrt{3}\sin\alpha) \,+\, } \color{blue}{ \sin^2\beta \, \frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}}} \color{blue}{ \left[ \frac{D(\cos\alpha \,+\, \sqrt{3}\sin\alpha)}{2\sqrt{3}} \,-\, \frac{1}{\sqrt{3}} \,+\,\frac{1\,-\,2\,D\cos\alpha}{2\sqrt{3}}\right]}\,-\, \color{green}{\frac{D^2}{4}} \,=\,0 \\ \color{blue}{ -2D^2 \,-\, D\,(\cos\alpha \,+\, \sqrt{3}\sin\alpha) \,+\, 1 \,-\, \sin^2\beta \,(1 \,-\, 2\,D\,\cos\alpha) \,} \color{blue}{ \left[ 1 \,+\, D\,(\cos\alpha \,+\, \sqrt{3}\sin\alpha) \right] \,=\, 0 \quad(Eq.2)} [/math]
Equations 3 and 4
[math] \\ \text{Equations 3 and 4 are trigonometric operators defining gamma letters:} \;\color{red}{\gamma}\;\text{and}\;\color{blue}{\Gamma} \\ \color{red}{\gamma \,\equiv\,\sqrt{3}\,\tan\alpha} \quad \color{blue}{\Gamma \,\equiv\,3\cos\alpha-\sqrt{3}\,\sin\alpha} \\ \color{blue}{\cos^2\alpha} \,+\, \color{red}{\sin^2\alpha} \,=\, 1 \,=\, \color{blue}{\cos^2\alpha \left(1 \,+\, \color{red}{\frac{\gamma^2}{3}}\right) } \quad or \quad \color{blue}{ \cos^2\alpha\,=\,\frac{1}{ 1 \,+\, \color{red}{ \frac{\gamma^2}{3}} }} \\ \color{blue}{ \Gamma\,\cos\alpha \,=\, (\cos\alpha -\color{red}{\sqrt{3}\sin\alpha}) \cos\alpha }\,=\, \color{blue}{ (3 \,-\, \color{red}{\gamma}) \, \cos^2\alpha \,=\, \frac{3\,-\,\color{red}{\gamma}}{1 \,+\, \color{red}{ \frac{\gamma^2}{3}} }} \\ \color{red}{ 3 \left( 1 \,+\, \frac{\gamma^2}{3} \right)} \color{red}{ \left[ \color{blue}{\Gamma\,\cos\alpha\,-\,} \color{blue}{ \frac{3\,-\,\color{red}{\gamma}}{1 \,+\, \color{red}{ \frac{\gamma^2}{3}} }} \right]} \,=\, \color{red}{ \overbrace{\Gamma\,\cos\alpha}^{a}\;\gamma^2 \,+\, \overbrace{3}^{b}\;\gamma + \overbrace{3( \Gamma\,\cos\alpha\,-\,3)}^{c} }\,=\,0 \\ Positive\,Root:\;\color{red}{ \gamma \,=\, \frac{-b+\sqrt{b^2-4\,a\,c}}{2\,a} } = \color{red}{ \frac{ -3 + \sqrt{ 9-12\,\Gamma\cos\alpha(\Gamma\cos\alpha -3)}}{2\Gamma\,\cos\alpha} \quad(Eq.3) } \\ \color{blue}{ \Gamma^2 \,=\, \Gamma\,\cos\alpha \,(3 - \gamma) }\,=\, \color{blue}{ 3\Gamma\,\cos\alpha - \frac{1}{2}\left[ -3 + \sqrt{ 9-12\,\Gamma\cos\alpha(\Gamma\cos\alpha -3)} \right] \quad (Eq. 4)} [/math]
Equation 5
Combine Equations 1 and 2 with variable y to solve between D and α [math] \\ \color{Goldenrod}{ Golden\,Ratio\,phi:\;\varphi\,\equiv\, \frac{1+\sqrt{5}}{2} } \quad\quad \color{Goldenrod}{\varphi^{n+2}+\varphi^{n-2}=3\varphi^{n}} \\ \color{red}{ Icosa\,symmetry:\;\sin^2\beta\,=\,\frac{1}{3\varphi^2}} \quad\quad \color{blue}{Combine:}\quad\color{blue}{ 3\varphi^2(Eq.2)} \;+\; \color{red}{3\varphi^2(Eq.1) \color{green}{y}} \,=\,0 \\ \color{green}{\overbrace{\left[3\varphi^2(y-2)+2\left((1-2y)\cos\alpha-\sqrt{3}\sin\alpha\right)\cos\alpha\right]}^{i}\,D^2 \,-\,} \color{green}{\overbrace{\left((4y+1)\cos\alpha+\sqrt{3}\sin\alpha\right)\varphi^4}^{j}\,D\;+} \color{green}{\overbrace{(y+1)\varphi^4}^{k}}\,=\,0 \\ \color{green}{Define}\,\color{red}{eta}\,and\,\color{blue}{lambda:}\; \color{green}{j^2-4ik \,\equiv\,(} \color{red}{\eta}\color{green}{\cos\alpha\,+\,} \color{blue}{\lambda}\color{green}{\sqrt{3}\sin\alpha)^2\;=\;} \color{blue}{\eta^2}\color{green}{\cos^2\alpha\,+\,} \color{red}{(\eta\lambda)} \color{green}{2\sqrt{3}\cos\alpha\sin\alpha +} \color{blue}{\lambda^2}\color{green}{3\sin^2\alpha} \\ \color{blue}{ \underbrace{ \left[ \varphi^2(4y+1)^2-4\varphi^2(y+1)\left(3\varphi^2(y-2)+2(1-2y)\right)\right]}_{\eta^2} } \color{green}{\cos^2\alpha \,+\,} \color{red}{ \underbrace{ \left[ \varphi^8(4y+1)+4\varphi^4(y+1) \right]}_{(\eta\lambda)} } \color{green}{2\sqrt{3}\cos\alpha\sin\alpha \,+\,} \color{blue}{ \underbrace{ \left[ \varphi^8-4\varphi^6(y+1)(y-2) \right]}_{\lambda^2} } \color{green}{3\sin^2\alpha} \\ Sum\,components \quad\quad \color{red}{(\eta\lambda)^2} \color{blue}{-\eta^2\lambda^2}\,=\,0 \\ \begin{subarray}{l} \\ \color{Goldenrod}{\varphi^{16}} &\|&&\|&&\|\; \color{red}{16}-\color{blue}{16} &&\|\; \color{red}{8}-\color{blue}{8} &&\|\; \color{red}{1}-\color{blue}{1} \\ \color{Goldenrod}{\varphi^{14}} &\|\; \color{blue}{64} &&\|\; \color{blue}{-32}\quad &&\|\; \color{blue}{-144} &&\|\; \color{blue}{-80} & \color{green}{144} &\|\; \color{blue}{-32} & \color{green}{-144} \\ \color{Goldenrod}{\varphi^{12}} &\|\; \color{blue}{-48}\quad & \color{green}{144}\; &\|\; \color{blue}{96} & \color{green}{0}\; &\|\; \color{red}{32} \color{blue}{+128}\quad & \color{green}{-288} &\|\; \color{red}{40} \color{blue}{-200} &&\|\; \color{red}{8} \color{blue}{-184}\quad & \color{green}{\;144} \\ \color{Goldenrod}{\varphi^{10}} &\|\; \color{blue}{64} &&\|\; \color{blue}{-32} &&\|\; \color{blue}{-192} &&\|\; \color{blue}{-32} &&\|\; \color{blue}{64} \\ \color{Goldenrod}{\varphi^{8}} &\|&&\|&&\|\; \color{red}{16} &&\|\; \color{red}{32} &&\|\; \color{red}{16} \\ \color{Goldenrod}{\div144\varphi^{12}} &\|& \color{green}{y^4} &\|& &\|& \color{green}{-2y^2\;} &\|& \color{green}{-\varphi^2 y\;} &\|& \color{green}{\;-\varphi} \end{subarray} \\ \begin{subarray}{lc} \color{red}{First\,root\,of\,y:\;-1} &&&\color{blue}{y^3} &\color{blue}{\overbrace{-y^2}^{p=-1}} &\color{blue}{\overbrace{-y}^{q=-1}} &\color{blue}{\overbrace{-\varphi}^{r=-\varphi}} \\ \color{blue}{a=\frac{-p^2}{3}+q\;=\; \frac{-1}{3}-1\;=\;\frac{-4}{3} }\; \color{Goldenrod}{(a=\frac{2}{3}\,plotted\,in\,book)} & \color{red}{(y+1)} &\quad \color{green}{\overline{|\;y^4}} \quad&&\quad\color{green}{-2y^2} \quad&\quad\color{green}{-\varphi^2y} \quad&\color{green}{-\varphi} \\ \color{blue}{b=\frac{2p^2}{27}-\frac{pq}{3}+r} \quad&& \color{green}{y^4} & \color{green}{+y^3} \\ \color{blue}{b=-\frac{2}{27}-\frac{1}{3}-\varphi \;=\; \frac{-49-27\sqrt{5}}{54}} \quad&& \color{green}{0} & \color{green}{-y^3} & \color{green}{-y^2} \\ \color{blue}{Second\,root\,of\,y:} \quad&&& \color{green}{0} & \color{green}{-y^2} & \color{green}{-y} \\ \color{blue}{\frac{-p}{3} -\sqrt[3]{ \frac{b}{2}+\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} -\sqrt[3]{ \frac{b}{2}-\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} \;=\; \xi^2-\frac{1}{3}} \quad&&&& \color{green}{0} & \color{green}{-\varphi y} & \color{green}{-\varphi} \\ \color{Goldenrod}{ Define\,Xi:\;\xi\,\equiv\,} \color{Goldenrod}{ \sqrt[3]{ \frac{\varphi}{2} + \frac{1}{2} \sqrt{ \varphi-\frac{5}{27}}}\;+\;} \color{Goldenrod}{ \sqrt[3]{ \frac{\varphi}{2} - \frac{1}{2} \sqrt{ \varphi-\frac{5}{27}}}} \quad&&&&& \color{green}{0} & \color{green}{0} \end{subarray} \\ [/math]
[math] \color{red}{From\,the\,first\,root\,of\,y:} \frac{ \color{blue}{(Eq.2)} -\color{red}{(Eq.1)}}{\color{green}{D}}\;=\;0 \\ \color{green}{ \left[ 2(3\cos\alpha-\sqrt{3}\sin\alpha)\cos\alpha-9\varphi^2\right] D \;+\; \varphi^4(3\cos\alpha-\sqrt{3}\sin\alpha)}\;=\; \color{green}{\left[ 2\Gamma\cos\alpha-9\varphi^2\right] D \;+\; \varphi^4\Gamma}\;=\;0 \\ \color{green}{D\;=\;\frac{ \varphi^4\Gamma}{9\varphi^2 - 2\Gamma\cos\alpha} \quad(Eq.5)} [/math]
Equation 6
[math] \color{red}{\frac{ \Gamma(9\varphi^2 - 2\Gamma\cos\alpha)}{ 3\varphi^2D} (Eq.1)} \;=\;0 \quad\color{green}{(substitute\,D\,with\,Eq.5)} \\ \color{red}{ \frac{ \Gamma(9\varphi^2 - 2\Gamma\cos\alpha)}{ 3\varphi^2}} \color{red}{\left[ (3\varphi^2-4\cos^2\alpha) \color{green}{ \left( \frac{ \varphi^4\Gamma}{9\varphi^2-2\Gamma\cos\alpha} \right)} -4\varphi^4\cos\alpha+\varphi^4 \color{green}{ \left( \frac{9\varphi^2-2\Gamma\cos\alpha}{ \varphi^4\Gamma} \right)} \right]} \;=\;0 \\ \color{red}{4(\Gamma\cos\alpha)^2 - 36\varphi^2\Gamma\cos\alpha + 27\varphi^2 + \varphi^4\Gamma^2} \;=\;0 \quad\color{blue}{(substitute\,\Gamma^2\,with\,Eq.4)} \\ \color{red}{4(\Gamma\cos\alpha)^2 + 3\varphi^2(\color{blue}{\varphi^4}-12)\Gamma\cos\alpha + \frac{3}{2}\varphi^2(\color{blue}{\varphi^2}+18)}\;=\; \color{blue}{ \frac{\varphi^4}{2}\sqrt{9-12\Gamma\cos\alpha(\Gamma\cos\alpha - 3)}} \\ \color{green}{\text{Square both sides and subtract}} \\ \color{green}{16(\Gamma\cos\alpha)^4 + 24\varphi^2(\varphi^2-12)(\Gamma\cos\alpha)^3 + 36\varphi^2(21\varphi^2 + 11)(\Gamma\cos\alpha)^2 + 54\varphi^4(\varphi^2-36)\Gamma\cos\alpha + 81\varphi^4(\varphi^2+9)}\;=\;0 \\ \color{green}{ Define\;x:\quad x\equiv\frac{2}{3}\Gamma\cos\alpha \quad \text{ and divide by 81:}} \\ \color{green}{x^4 + \varphi^2(\varphi^2-12)x^3 + \varphi^2(21\varphi^2+11)x^2 + \varphi^4(\varphi^2-36)x + \varphi^4(\varphi^2+9)}\;=\;0 \\ [/math] [math] \begin{subarray}{lc} \color{red}{First\,root\,of\,x:\;1} &&&\color{blue}{x^3} &\color{blue}{\overbrace{-9\varphi^2}^{p=-9\varphi^2}x^2} &\color{blue}{\overbrace{+\varphi^2(21\varphi^2+2)}^{q=\varphi^2(21\varphi^2+2)}x} &\color{blue}{\overbrace{-\varphi^4(\varphi^2+9)}^{r=-\varphi^4(\varphi^2+9)}} \\ \color{blue}{a=\frac{-p^2}{3}+q\;=\; -27\varphi^4+\varphi^2(21\varphi^2+2) \;=\; -2\varphi^6 } & \color{red}{(x-1)} &\quad \color{green}{\overline{|\;x^4}} \quad&\quad\color{green}{+\varphi^2(\varphi^2-12)x^3} \quad&\quad\color{green}{+\varphi^2(21\varphi^2+11)x^2} \quad&\color{green}{+\varphi^4(\varphi^2-36)x} \quad&\color{green}{+\varphi^4(\varphi^2+9)} \\ \color{blue}{b=\frac{2p^2}{27}-\frac{pq}{3}+r} \quad&& \color{green}{x^4} & \color{green}{-x^3} \\ \color{blue}{b=-54\varphi^6 + 3\varphi^4(21\varphi^2+2) - \varphi^4(\varphi^2+9)\;=\;{\huge \color{Goldenrod}{\varphi^{10}}}} \quad&& \color{green}{0} & \color{green}{-9\varphi^2x^3} & \color{green}{+9\varphi^2x^2} \\ \quad&&& \color{green}{0} & \color{green}{\varphi^2(21\varphi^2+2)x^2} & \color{green}{-\varphi^2(21\varphi^2+2)x} \\ \color{blue}{Second\,root\,of\,x:} \quad&&&& \color{green}{0} & \color{green}{-\varphi^4(\varphi^2+9)x} & \color{green}{\varphi^4(\varphi^2+9)} \\ \color{blue}{\frac{-p}{3} -\sqrt[3]{ \frac{b}{2}+\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} -\sqrt[3]{ \frac{b}{2}-\sqrt{ \frac{b^2}{4}+\frac{a^3}{27}}} \;=\; 3\varphi^2-\varphi^3\xi} &&&&& \color{green}{0} & \color{green}{0} \\ \end{subarray} \\ \color{blue}{\text{From the second root of x:} \quad \Gamma\cos\alpha \;=\; \frac{3}{2}(3\varphi^2-\varphi^3\xi)\quad(Eq.6) } \\ [/math]
Equation 7
[math] \color{green}{ \left( \sqrt[3]{ \frac{\varphi}{2} + \sqrt{ \frac{\varphi^2}{4}-\frac{8}{27}}}\right)} \color{green}{ \left( \sqrt[3]{ \frac{\varphi}{2} - \sqrt{ \frac{\varphi^2}{4}-\frac{8}{27}}}\right)} \color{green}{\;=\; \sqrt[3]{\frac{8}{27}} \;=\; \frac{2}{3} \quad so, \quad \xi^3 = 2\xi + \varphi\quad(Eq.7)} \\ [/math]
Equation 8
[math]
\color{green}{Noting\;D\,=\, \sqrt{3}\sin\alpha-\cos\alpha, \;we\,find:}
\\
\quad\color{red}{ (9\varphi^3+\varphi+6\xi-3\varphi^3\xi^2)^2}
\color{blue}{ -(\varphi+3\xi)^2 \left(1-3\varphi^4(3\sqrt{5}-2\varphi^3\xi + \varphi^2\xi^2)\right)} \;=\;0
\quad\color{green}{(expand\,and\,substitute\,\xi^3\,with\,Eq.7)}
\\
\color{green}{=\;}
\color{red}{(9\varphi^3+\varphi)^2 + 36\xi^2 +9\varphi^6\xi\color{green}{(2\xi+\varphi)}+2(9\varphi^3+\varphi)(6\xi-3\varphi^3\xi^2)}
\color{red}{-36\varphi^3} \color{green}{(2\xi+\varphi)}
\color{blue}{ -\varphi^2 \left(1-3\varphi^4(3\sqrt{5} - 2\varphi^3\xi + \varphi^2\xi^2) \right)}
\\
\quad\color{blue}{-6\varphi \left( \xi-3\varphi^4 \left( 3\sqrt{5}\xi - 2\varphi^3\xi^2 + \varphi^2\color{green}{(2\xi+\varphi)} \right)\right)}
\color{blue}{-9 \left( \xi^2-3\varphi^4 \left( 3\sqrt{5}\xi^2 - 2\varphi^3\color{green}{(2\xi+\varphi)}
+ \varphi^2\xi\color{green}{(2\xi+\varphi)} \right)\right)}\;=\;0
\\
\color{green}{=\;(}
\color{red}{81\varphi^6+18\varphi^4+\varphi^2-36\varphi^4} \color{blue}{-\varphi^2+9\varphi^6\sqrt{5}+18\varphi^8-54\varphi^8}
\color{green}{)\quad\quad\text{(all 3 orders of}\;\xi\;\text{sum to zero)}}
\\
\quad\color{green}{+\;(}
\color{red}{9\varphi^7+12(9\varphi^3+\varphi)-72\varphi^3}
\color{blue}{+6\varphi^9-6\varphi +54\varphi^5\sqrt{5}+36\varphi^7-108\varphi^8+27\varphi^7}
\color{green}{)\xi}
\\
\quad\quad\color{green}{+\;(}
\color{red}{36+ 18\varphi^6-6\varphi^3(9\varphi^3+\varphi)}
\color{blue}{+3\varphi^8-36\varphi^8-9 + 81\varphi^4 \sqrt{5}+54\varphi^6}
\color{green}{)\xi^2}\;=\;0
\\
[/math]
[math]
\color{blue}{\sqrt{1-3\varphi^4(3\sqrt{5}-2\varphi^3\xi+ \varphi^2\xi^2)}}
\color{red}{\;=\;\frac{9\varphi^3+\varphi+6\xi-3\varphi^3\xi^2}{\color{blue}{\varphi +3\xi}}}
\quad\color{blue}{(Eq.8)}
\\
[/math]
Solve for cos α
[math] \\ \color{green}{Substitute\color{blue}{Eq.6}\,and\,\color{blue}{Eq.8}\,into\,\color{red}{Eq.3}} \\ \color{red}{\gamma\;=\; \frac{ -3 + \sqrt{ 9-12\,\Gamma\cos\alpha(\Gamma\cos\alpha -3)}}{2\Gamma\,\cos\alpha}} \color{blue}{ \;=\;\frac{ -1+\sqrt{ 1-3\varphi^4(3\sqrt{5}-2\varphi^3\xi+\varphi^2\xi^2)}}{3\varphi^2-\varphi^3\xi} } \color{blue}{ \;=\;\frac{ -1+ \color{red}{\frac{9\varphi^3+\varphi+6\xi-3\varphi^3\xi^2}{\color{blue}{\varphi +3\xi}}}}{ 3\varphi^2-\varphi^3\xi}} \\ \color{red}{\gamma\;=\; \frac{ \color{blue}{-\varphi -3\xi} +9\varphi^3 +\varphi +3\xi +3(3\varphi^2 - \varphi^4)\xi -3\varphi^3\xi^2} {\color{blue}{(\varphi +3\xi)(3\varphi^2 -\varphi^3\xi) }}} \color{red}{\;=\;\frac{3\varphi+3\xi}{\varphi+3\xi}} \\ \color{blue}{ \cos\alpha \;=\; \frac{1}{ \sqrt{ 1\color{red}{+\tan^2\alpha}}}} \;=\; \color{blue}{ \frac{1}{ \sqrt{ 1\color{red}{ +\frac{\gamma^2}{3} }}}} \;=\; \color{blue}{ \frac{1}{ \sqrt{ 1\color{red}{ +\frac{1}{3}\left( \frac{3\varphi+3\xi}{\varphi+3\xi} \right)^2}}}} \;=\; \color{blue}{ \frac{\varphi+3\xi}{2\sqrt{ \varphi^2+3\xi(\varphi+\xi)}}} \\ [/math]
Equation 9
[math] \color{blue}{ \Gamma\;=\;\cos\alpha[3\color{red}{-\gamma}]} \color{blue}{ \;=\; \left( \frac{\varphi+3\xi}{2\sqrt{ \varphi^2+3\xi(\varphi+\xi)}} \right) } \color{blue}{ \left[ 3\color{red}{-\frac{3\varphi+3\xi}{\varphi+3\xi}} \right] } \color{blue}{ \;=\; \frac{3\xi}{\sqrt{ \varphi^2+3\xi(\varphi+\xi)}} \quad(Eq.9)} \\ [/math]
Solve for D
[math] \\ \color{green}{Substitute\;\color{blue}{Eq.6}\;and\;\color{blue}{Eq.9}\;into\,Eq.5} \\ \color{green}{D\;=\;\frac{ \varphi^4\Gamma}{9\varphi^2 - 2\Gamma\cos\alpha}} \color{green}{\;=\;\frac{\varphi\Gamma}{3\xi}} \color{green}{ \;=\; \frac{\varphi}{\sqrt{ \varphi^2+3\xi(\varphi+\xi)}}} \\ [/math]
Solve for Volume
[math] \color{red}{Icosa\,symmetry:}\; \color{blue}{\cos\beta=\frac{\varphi}{\sqrt{3}}} \quad \color{red}{ \sin\beta=\frac{1}{\varphi\sqrt{3}}} \quad \color{blue}{\overline{a\color{green}{b}}=\frac{1}{2\sqrt{3}}} \quad \color{blue}{\overline{ac}=\frac{\overline{a\color{green}{b}}}{\tan\beta}= \frac{\varphi^2}{2\sqrt{3}}} \\ \color{green}{ \text{Radius to triangle face:}\;r_{triangle}\;=\; \frac{\color{blue}{\overline{ac}}}{\color{green}{D}}} \color{green}{ \;=\; \frac{\varphi}{2\sqrt{3}}\sqrt{ \varphi^2+3\xi(\varphi+\xi)}} \\ \color{green}{ \text{Circumradius (radius to vertex):}} \\ \color{green}{r_{circumradius}\;=\; \sqrt{ \color{blue}{r^2_{triangle}} \color{red}{+(2\sin\frac{\pi}{3})^{-2}} }} \color{green}{ \;=\; \sqrt{ \frac{ \color{blue}{\varphi^2\left(\varphi^2 + 3\xi(\varphi+\xi)\right)} \color{red}{+ 4}}{12} }} \color{green}{ \;=\; \frac{1}{2}\sqrt{ \frac{ \varphi^4 + 4 +3\varphi^2\xi(\varphi+\xi) }{3}}} \\ \color{green}{ \text{Inradius (radius to pentagon face):}} \\ \color{green}{r_{pentagon}\;=\; \sqrt{ \color{blue}{r^2_{circumradius}} \color{red}{-(2\sin\frac{\pi}{5})^{-2}} }} \color{green}{ \;=\; \sqrt{ \frac{ \color{blue}{ \varphi^4 + 4 +3\varphi^2\xi(\varphi+\xi) } }{12} \color{red}{-\frac{\varphi}{\sqrt{5}}} }} \color{green}{ \;=\; \frac{\varphi}{2}\sqrt{ \frac{1}{\varphi\sqrt{5}}+\xi(\varphi+\xi)}} \\ \color{green}{ \text{Midradius (radius to edge bisector):}} \\ \color{green}{r_{midradius}\;=\; \sqrt{ \color{blue}{r^2_{triangle}} +(2\tan\frac{\pi}{3})^{-2} }} \color{green}{ \;=\; \sqrt{ \frac{ \color{blue}{\varphi^2\left(\varphi^2 + 3\xi(\varphi+\xi)\right)} + \color{red}{1} }{12} }} \color{green}{ \;=\; \frac{1}{2}\sqrt{ \frac{ \varphi^4 + 1 +3\varphi^2\xi(\varphi+\xi) }{3}}} \\ \color{red}{Volume_{Snub Dodecahedron}\;=\;} \color{blue}{N_{triangle}\times Area_{triangle}\times\frac{1}{3} \times r_{triangle} } \color{green}{+N_{pentagon}\times Area_{pentagon}\times\frac{1}{3} \times r_{pentagon} } \\ \quad\color{red}{=\;} \color{blue}{ 80\frac{\sqrt{3}}{4}\frac{1}{3}\frac{\varphi}{2\sqrt{3}}\sqrt{ \varphi^2+3\xi(\varphi+\xi)}} \color{green}{\,+\,12\frac{5}{4}\sqrt{\frac{\varphi^3}{\sqrt{5}}}\frac{1}{3} \frac{\varphi}{2}\sqrt{ \frac{1}{\varphi\sqrt{5}}+\xi(\varphi+\xi)} } \\ \color{red}{Volume_{Snub Dodecahedron}\;=\;} \quad\color{red}{=\;} \color{red}{\frac{10\varphi}{3}\sqrt{ \varphi^2+3\xi(\varphi+\xi)}} \color{red}{\,+\,\frac{\varphi^2}{2}\sqrt{ 5 + 5\sqrt{5}\varphi\xi(\varphi+\xi)} } \\ [/math]
Notes
- ↑ Weisstein, Eric W. "Snub Dodecahedron." From MathWorld--A Wolfram Web Resource.
- ↑ J J O'Connor, E F Robertson "Pappus of Alexandria." MacTutor
- ↑ J J O'Connor, E F Robertson "Archimedes." MacTutor
- ↑ Weisstein, Eric W. "Archimedean Solid." From MathWorld--A Wolfram Web Resource.
- ↑ Weisstein, Eric W. "Schlaefli Symbol." From MathWorld--A Wolfram Web Resource.
- ↑ Peter Schreiber, Gisela Fischer & Maria Luise Sternath. "Rediscovery of the Archimedean solids during the Renaissance." Springer
- ↑ J J O'Connor, E F Robertson "Luca Pacioli." MacTutor
- ↑ Luca Pacioli "De divina proportione." Archive.org
- ↑ Daniel A. Di Liscia. "Johannes Kepler." Stanford Encyclopedia of Philosophy
- ↑ Kepler, Johannes "Harmonices Mundi." 1619. Archive.Org
- ↑ *Coxeter, H. S. M.; Longuet-Higgins, M. S.; and Miller, J. C. P. "Uniform Polyhedra." Phil. Trans. Roy. Soc. London Ser. A 246, 401-450, 1954.
- ↑ Mark Adams. "Snub Dodecahedron Volume." Wolfram Cloud Notebook
- ↑ Geometry Loses One of Its Most Eloquent Expositors
- ↑ About Eric Weisstein, Creator of MathWorld
- ↑ Harish Chandra Rajpoot, H. C. R. “Optimum Solution of Snub Dodecahedron (an Archimedean Solid) by Using HCRs Theory of Polygon & Newton-Raphson Method.” 2015. Research Gate
- ↑ Adams, Mark S. “Archimedean & Platonic Solids.” 1985. Archive.Org
Other
- Pacioli, Luca. "Divina proportione" 1509. Archive.Org
- Kepler, Johannes "Harmonices Mundi." 1619. Archive.Org
- Coxeter, H. S. M.; Longuet-Higgins, M. S.; and Miller, J. C. P. "Uniform Polyhedra." Phil. Trans. Roy. Soc. London Ser. A 246, 401-450, 1954. Royal Society Publishing
- Weisstein, Eric W. "Snub Dodecahedron." MathWorld--A Wolfram Web Resource
- Harish Chandra Rajpoot, H. C. R. “Optimum Solution of Snub Dodecahedron (an Archimedean Solid) by Using HCRs Theory of Polygon & Newton-Raphson Method.” 2015. Research Gate
Python code supplement to Conservapedia page on Snub Dodecahedron Calculations of the volume of the Snub Dodecahedron five ways
